2005-11-01
Abstract
'Over 99% accurate!' 'Zero critical false positives!' '10 times more effective than a human!' Claims about the accuracy of spam filters abound in marketing literature and on company websites. Yet even the term 'accuracy' isn't accurate.
Copyright © 2005 Virus Bulletin
'Over 99% accurate!' 'Zero critical false positives!' '10 times more effective than a human!' Claims about the accuracy of spam filters abound in marketing literature and on company websites. Yet even the term 'accuracy' isn't accurate. The phrase '99% accurate' is almost meaningless; 'critical false positives' are subjective; and claims about being better than humans are hard to interpret when based on an unreliable calculation of accuracy.
Before explaining what's wrong with the figures that are published for spam filter accuracy, and describing some figures that actually do make sense, let's get some terminology clear.
The two critical terms are 'spam' and 'ham'. The first problem with measuring a spam filter is deciding what spam is. There are varying formal definitions of spam, including unsolicited commercial email (UCE) and unsolicited bulk email (UBE). But to be frank, no formal definition captures people's common perception of spam; like pornography, the only definition that does work is 'I know it when I see it'.
That may be unsatisfactory, but all that matters in measuring a spam filter's accuracy is to divide a set of email messages into two groups: messages that are believed to be spam and those that are not (i.e. legitimate messages, commonly referred to as 'ham').
With spam and ham defined, it is possible to define two critical numbers: the false positive rate and the false negative rate. In the spam filtering world these terms have specific meanings: the false positive rate is the percentage of ham messages that were misidentified (i.e. the filter thought that they were spam messages); the false negative rate is the percentage of spam messages misidentified (i.e. the filter thought that they were legitimate).
To be formal, imagine a filter under test that receives S spam messages and H ham messages. Of the S spam messages, it correctly identifies a subset of them with size s; of the ham messages it correctly identifies h of them as being ham. The false positive rate of the filter is:
(H – h)/ H
The false negative rate is:
(S – s)/ S
An example filter might receive 7,000 spams and 3,000 hams in the course of a test. If it correctly identifies 6,930 of the spams then it has a false negative rate of 1%; if it misses three of the ham messages then its false positive rate is 0.1%.
How accurate is that filter? The most common definition of accuracy used in marketing anti-spam products is the total number of correctly identified messages divided by the total number of messages. Formally, that is:
( s + h) / ( S + H)
or, in this case 99.27%.
99.27% sounds pretty good when marketing, but this figure is meaningless. A product that identified all 7,000 spams correctly, but missed 73 hams (i.e. has a false positive rate of 2.43%) is also 99.27% accurate.
And therein lies the reason why 'accuracy' is useless. Since spam filters quarantine or delete messages they believe to be spam, a false positive is unseen by the end user. And a false positive is a legitimate (often business-related) email that has been lost. If you had to chose between a filter that loses 1 in 1,000 hams or one that loses nearly 1 in 40, you'd surely chose the former. The difference in importance between missed spam and missed ham reflects a skew in the cost of errors. (For a longer discussion of methods of calculating a spam filter's performance numbers see VB, May 2005, p.S1.)
While I'm on the subject of meaningless marketing words, take a look at 'critical false positives' (CFPs). A critical false positive is apparently a false positive that you care about. Anti-spam filter vendors like to divide ham messages into two groups: messages that you really don't want to lose, and those that it would be OK to lose. The handwaving definition of these two groups tends to be 'business messages' and 'personal messages and opt-in mailing lists'. Given that it's impossible to define a critical false positive, spam filter vendors have incredible latitude in defining what is and is not a CFP, and hence CFP percentages are close to useless.
In my anti-spam tool league table (ASTLT, see http://www.jgc.org/astlt/) – which summarizes published reports of spam filter accuracy – I use two numbers: the spam hit rate (which is the percentage of spam caught: 100% – false negative rate, or s/S) and the ham strike rate (the percentage of ham missed, i.e. the false positive rate).
A typical entry in the ASTLT looks like this:
| hghfghgfh | Spam hit rate | Ham strike rate |
|---|---|---|
| MegaFilterX | .9956 | .0010 |
This means that MegaFilter X caught 99.56% of spam and missed 0.1% of ham. The table is published in three forms: sorted by spam catch rate (best to worst, i.e. descending); sorted by ham strike rate (best to worst, i.e. ascending); and grouped by test. (Entries in the ASTLT are created from published reports of spam filter tests in reputable publications. The full details are provided on the ASTLT website. It is important to note that it's difficult to compare the numbers from different tests because of different test methodologies.)
The top five solutions from the current ASTLT figures (where top is defined by maximal spam hit rate and minimal ham strike rate) are:
| Tool | Spam hit rate | Ham strike rate |
|---|---|---|
| GateDefender | .9954 | .0000 |
| IronMail | .9880 | .0000 |
| SpamNet | .9820 | .0160 |
| CRM114 | .9756 | .0039 |
| SpamProbe | .9657 | .0014 |
Here, the 'best' filter is the one with the highest spam hit rate and lowest ham strike rate. In the sample of entries above GateDefender is overall best, with IronMail close behind.
The use of two numbers also means that charts can easily be drawn where the upper right-hand corner indicates the best performance. All that is necessary is to plot the spam catch rate along the X axis and the ham strike rate along the Y axis (albeit in reverse order). Figure 1 shows the position of the top five solutions in the ASTLT.
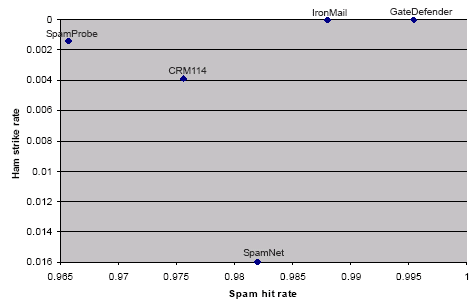
Figure 1. Spam hit rate and ham strike rate for the top five solutions from the current ASTLT. The upper right-hand corner of the chart indicates the best performance.
However, testing organizations such as VeriTest (http://www.veritest.com/) wish to publish a single figure giving the overall performance of a spam filter. The simplest way to do this is to combine the spam hit rate and ham strike rate by weighting the contribution that those two numbers make to an overall 'performance' score for the filter. Clearly, the way in which the weights are created needs to reflect how much importance an end user gives to missed ham vs. delivered spam.
In VeriTest's case the spam hit rate contributes 40% of the overall score and the ham strike rate contributes 60%. To achieve the final score, the first thing they do is to translate each of the percentages into a score on the scale 2 to 5.
| Spam hit rate | VeriTest points |
|---|---|
| At least .9500 | 5 |
| Between .9000 and .9500 | 4 |
| Between .8500 and .9000 | 3 |
| Less than .8500 | 2 |
For the spam hit rate the top score, 5, comes at greater than .9500:
| Ham strike rate | VeriTest points |
|---|---|
| Less than .0050 | 5 |
| Between .0050 and .0100 | 4 |
| Between .0100 and .0150 | 3 |
| Greater than .0150 | 2 |
VeriTest then takes the two 'VeriTest points' for a filter and combines them to obtain a final score (between 2 and 5), with 40% contributed by the spam hit rate and 60% by the ham strike rate.
Score = (spam hit rate points * 0.4) + (ham strike rate points * 0.6)
(For more on VeriTest's methodology see: http://www.veritest.com/downloads/services/antispam/VeriTest_AntiSpam_Benchmark_Service_Program_Description.pdf).
Using that scheme it's possible to score the top five tools in the ASTLT:
| Tool | Spam hit rate | Ham strike rate | SHR strike rate | HSR points | Score |
|---|---|---|---|---|---|
| GateDefender | .9954 | .0000 | 5 | 5 | 5 |
| IronMail | .9880 | .0000 | 5 | 5 | 5 |
| SpamNet | .9820 | .0160 | 5 | 2 | 3.2 |
| CRM114 | .9756 | .0039 | 5 | 5 | 5 |
| SpamProbe | .9657 | .0014 | 5 | 5 | 5 |
The combined scores put four of the tools on the same footing, and only SpamNet is scored lower because of its poor ham strike rate.
Part of the problem here is that there is no discrimination between spam filters once they reach a spam hit rate of .9500, or a ham strike rate of .0050. Better discrimination occurs if the scale is extended to 10 points, with the spam hit rate and ham strike rate broken down further.
The top score of 10 is given if the spam filter gives a perfect performance and misses no spam. Between .9500 and perfection each percentage point change (.0100) adds a point:
| Spam hit rate | Points |
|---|---|
| Perfect (i.e. 1) | 10 |
| Less than 1 | 9 |
| Between .9800 and .9900 | 8 |
| Between .9700 and .9800 | 7 |
| Between .9600 and .9700 | 6 |
| Between .9500 and .9600 | 5 |
| Between .9000 and .9500 | 4 |
| Between .8500 and .9000 | 3 |
| Less than .8500 | 2 |
Similarly, points for the ham strike rate can be extended to 10, breaking down ham strike rates below .0050 every tenth of a percentage (.0010):
| Ham strike rate | Points |
|---|---|
| Perfect (i.e. 0) | 10 |
| Less than .0010 | 9 |
| Between .0010 and .0020 | 8 |
| Between .0020 and .0030 | 7 |
| Between .0030 and .0040 | 6 |
| Between .0040 and .0050 | 5 |
| Between .0050 and .0100 | 4 |
| Between .0100 and .0150 | 3 |
| Greater than .0150 | 2 |
Now rescoring the top five tools using the same weighting (40% for spam catching ability and 60% for correct ham identification) a distinction emerges:
| Tool | Spam hit rate | Ham strike rate | SHR strike rate | HSR points | Score |
|---|---|---|---|---|---|
| GateDefender | .9954 | .0000 | 9 | 10 | 9.6 |
| IronMail | .9880 | .0000 | 8 | 10 | 9.2 |
| SpamNet | .9820 | .0160 | 8 | 2 | 4.4 |
| CRM114 | .9756 | .0039 | 5 | 6 | 6.4 |
| SpamProbe | .9657 | .0014 | 6 | 8 | 7.2 |
As spam filters improve, such discrimination between small changes in spam hit rate and ham strike rate are vital in determining which spam filter is the best.
Determining the right weights is difficult and subjective. Is a missed ham twice as bad as a missed spam, 10 times as bad? It's hard to know the answer. What is needed is a way of weighing the cost of an undelivered ham and the cost of a delivered spam.
To try to model that, imagine that an organization receives M messages per year, that Sp percent of the messages are spam, and that the organization has determined that a delivered spam costs Cs (you choose the currency) and an undelivered ham costs Ch.
The annual cost of a spam filter can be determined in terms of its spam hit rate (SHR) and ham strike rate (HSR) as follows:
Cost = Sp * M * Cs * (1-SHR) + (1-Sp) * M * Ch * HSR
It's possible to simplify that formula when comparing filters by first eliminating M, yielding a cost per message (CPM):
CPM = Sp * Cs * (1-SHR) + (1-Sp) * Ch * HSR
And then, instead of assigning absolute values to the costs of missed messages, replace Cs and Ch within their relative costs. By assigning the cost of a delivered spam a base value of 1 and an undelivered ham a relative cost of H the formula can be used to compare filters:
Simplified cost = Sp * (1-SHR) + (1-Sp) * H * HSR
And given that the percentage of all messages that are spam is well known (and probably knowable for a given organization), an absolute value for Sp can be inserted. Imagine that 65% of all messages are currently spam:
Simplified cost = 0.65 * (1-SHR) + 0.35 * H * HSR
Now for any spam filter's published or tested spam hit rate and ham strike rate it's possible to plot H against the simplified cost. In that way an organization can determine which filter to choose based on the sensitivity to changes in H.
Figure 2, for example, is a graph showing the cost of each of the top five spam filters in this article with H varying from 1 to 10 (i.e. a false positive is between 1 and 10 times the cost of a delivered spam):
Because GateDefender and IronMail had a ham strike rate of .0000 the cost is constant and GateDefender (with the best spam hit rate) is the cheapest overall. (In a real test it would be better to evaluate the actual spam hit rate and ham strike rate before plugging them into the formulae above; it's unlikely that a ham strike rate of .0000 is currently feasible in the real world).
An interesting cross over happens when H is around 7. At that point SpamProbe becomes cheaper to use than CRM114; this reflects SpamProbe's lower ham strike rate. SpamNet quickly becomes the most expensive solution because of its high ham strike rate.
Spam filters are becoming more and more accurate; they are catching more spam and missing less ham. But it is still important to weigh two numbers when evaluating a filter: its ability to catch spam and its effectiveness at delivering ham.
I am always on the look out for new tests to include in the league table; if you know of any please email them to me. The figures in this article are from the published test results that I know about; other tests may show that the products mentioned have better performance than indicated here.