F-Secure, Finland
Copyright © 2018 Virus Bulletin
Computer security is a serious issue which attracts the interest of all nations. Malicious codes are implemented to stay hidden both during the infection process and during the operation of the code, preventing their removal and the analysis of the code. The programs used today to detect malicious code, such as most anti-virus software and firewalls, are problematic as a version of the malicious program needs to have been analysed prior to the detection itself.
The reason the analysis process is necessary is that these security programs work using patterns that have been extracted from the malware, called signatures. Furthermore, at least one computer system needs to be infected in order for the code to be analysed. These kinds of software defences work well for detecting known malware, but they are no defence against new threat variants. The industry’s approach still relies heavily on the well-known technique of signature matching.
Software analysis is a critical point in dealing with malware, since most samples employ some sort of packing or obfuscation techniques in order to thwart analysis. It is also an area of economic concern in protecting digital assets from intellectual property theft.
Analysis tools help analysts identify vulnerabilities and issues before they can cause harm downstream. Understanding how software and hardware can be secured using tools and techniques beyond the standard debuggers and unit tests ensures greater security and integrity. This paper provides an introduction to some practical applications of SMT solvers in IT security, investigating the theoretical limitations and practical solutions, focusing on their use as a tool for binary static analysis.
Nowadays, most malware is programmed to stay hidden during infection and operation, preventing its removal and the analysis of its code. The current solutions used to detect malicious code, such as anti-virus software and firewalls, are problematic as prior information about the malicious code must be available in order for those programs to detect the code on a system. This is because these solutions work using patterns extracted from the malware called signatures. Therefore, at least one computer system needs to have been infected in order for the code to be analysed.
Static analysis of a piece of malicious code is a very demanding process. Usually, it’s done by a person (a security analyst) who will stare at one binary code for hours, searching for patterns – the signatures. Security analysts need tools to help them analyse new threats: since malware is distributed in compiled form, a disassembler is required. The process of analysing compiled code is the reverse process of software engineering and therefore called reverse engineering.
This paper will first introduce constraint programming to provide a background to how solvers work, after which it will describe the malware detection problem as a satisfiability problem, and finally present an algorithm to analyse malware using logic.
In this section, Constraint Programming (CP) and Constraint Satisfaction Problems (CSPs) will be explained and an overview of the most common solving techniques will be provided. According to Eugene C. Freuder in [1]:
‘CP represents one of the closest approaches computer science has yet made to the Holy Grail of programming: the user states the problem, the computer solves it.’
CP is a declarative programming paradigm which consists of the formulation of a solution to a problem as a CSP [2]. In the CSP a number of variables are introduced, with well-specified domains and which describe the state of the system. A set of relations, called constraints, is then imposed on the variables that make up the problem. These constraints are understood to have to hold true for a particular set of bindings for the variables, resulting in a solution to the CSP.
Constraints have some interesting properties when it is desirable to work in different environments, such as:
Constraint programming is devoted to solving constraint satisfaction problems. A CSP, P, is defined as a tuple (X, D, C), where [3]:
The size of vars(ci) is called the arity of the constraint ci. Constraints that have an arity of 2 are called binary. Constraints whose arity is greater than 2 are called non-binary. Every CSP can be converted into an equivalent binary CSP, where all constraints are binary [4]. The convenience of binary CSPs is that they can be represented by a constraint graph. In such graphs the nodes are labelled with the variable identifiers and the edges connect pairs of variables inside some of the constraint domains.
Each tuple τ ∈ rel(ci) is an ordered list of values (a1,··· ,ak) such that aj ∈ Din(xj),j = 1,··· ,k. A tuple is valid if all the values in the tuple are present in the domains of the corresponding variables. That means:
A solution to a CSP is an assignment (or a tuple) where every constraint is satisfied.
CSPs are also combinatorial problems that can be solved by search. Unfortunately, systematic search – such as ‘generate and test’ or ‘backtracking’ – is not usually feasible in practice. Therefore, one of the main research topics in the area of constraint satisfaction consists of finding efficient constraint-solving algorithms, like ‘consistency check’.
The process which verifies whether or not a given tuple is allowed by constraint ci is called a consistency check. Consistency check techniques were introduced to improve the efficiency of search algorithms [5]. A constraint can be defined either extensionally, by the set of allowed (or disallowed) tuples, or intensionally, by a predicate or arithmetic function.
Consistency check techniques can rule out many inconsistent tuples at a very early stage. Customarily, this is done by removing values from a variable’s domain. Once the domain of the variable becomes empty, we can ensure that the CSP has no solution, as the consistency of the algorithm fails to achieve consistency. However, the procedure is not complete, because even if the algorithm achieves consistency, it does not necessarily mean that the CSP has a solution.
Besides traditional search, there are a number of alternative methods for solving CSPs, each with varying levels of success. Among them, Satisfiability (SAT) and Satisfiability Modulo Theory (SMT) are two of the most promising for use in malware detection and binary analysis.
Satisfiability (SAT) basically consists of encoding CSPs into Boolean satisfiability problems. A Boolean satisfiability problem is the problem of determining whether the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to true. This means that SAT can be defined as a propositional formula.
A propositional formula is a formula composed from the propositional operators ¬,∨,∧,−→,←→ and a finite set, V, of Boolean valued variables.
An assignment or valuation is a map v : V → {false,true}. This assignment v is lifted to propositional formulas by defining the following:
A propositional formula θ is called satisfiable (SAT) if there exists a v such as v(θ) = true. Then v is called a satisfying assignment.
SAT was the first known example of an NP-complete problem.1 Nevertheless, thanks to better implementation techniques and improvement of concepts, such as conflict-driven lemma learning, these solvers are able to reduce the size of the search space significantly.
Satisfiability Modulo Theory (SMT), as the name implies, consists of encoding CSPs into SAT modulo theory problems. An SMT formula is a generalization of a Boolean formula, where some variables are replaced by predicates with predefined interpretations like simple arithmetic.
While the language of SAT solvers is Boolean logic, the language of SMT solvers is first-order logic. This language includes the Boolean operations using more complicated expressions involving constant, function, and predicate symbols instead of propositional variables. Expressions in first-order logic are made up of sequences of symbols. Symbols are divided into logical symbols and non-logical symbols or parameters.
The theory reasoning in an SMT solver is done with a theory solver. Given a Σ-theory T, a theory solver for T takes as input a set of Σ-literals and determines whether the set is satisfiable or unsatisfiable.
For example, a formula contains a clause such as a ∨ b ∨ (x + 5) ≤ y, where a and b are Boolean variables and x and y are integer variables. Such linear integer inequalities are evaluated according to the background theory [6].
A theory is, at first, a set of first-order formulas closed under logical consequence. That said, given a theory τ, τ is called decidable if there is an effective method for determining whether arbitrary formulas are included in τ.
A formula φ is called τ-satisfiable or τ-consistent if τ ∪ {φ} is satisfiable in the first-order sense. Otherwise, it is called τ-unsatisfiable or τ-inconsistent.
Accordingly, the SMT problem for a theory τ is the problem of determining, given a formula φ, whether φ is τ-satisfiable.
CSPs are most well researched in the artificial intelligence field, however they are not restricted to it. A well-known real-world constraint satisfaction problem is a simple multi-lingual translator tool, which combines two different problems: word-sense disambiguation – an open problem of natural language processing and ontology – and the machine reading comprehension [7].
In addition, almost all logic puzzles, such as the Rubik’s Cube and Sudoku puzzles, can be expressed as CSPs, and many solutions using SMT solvers can be found online. For those interested in reading more, [8] is a deeper analysis of Sudoku as a CSP.
Theoretical problems like Vertex-Cover and Graph KColorability (Chromatic Number) are also examples of more complex theoretical CSPs (where a set of start conditions exists in NP-Complete scope) [9].
Let’s consider the following systems of equations:
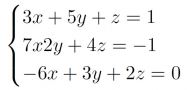
we can write in SMT2 language:
(declare-const x Real)
(declare-const y Real)
(declare-const z Real)
(assert (=(+(+ (* 3 x ) (* 5 y ) ) z ) 1))
(assert (=(+(+ (* 7 x) (* 2 y) ) (* 4 z)) (- 1)))
(assert (=(+(+ (* (- 6) x ) (* 3 y ) ) 2z ) 0))
(check-sat)
(get-model)
and this will output:
sat
(model
(define-fun z () Real
(- (/ 65.0 76.0)))
(define-fun y () Real
(/ 15.0 76.0))
(define-fun x () Real
(/ 11.0 38.0))
)
These are both solutions for our systems of equation.2
Numerous definitions have been offered to describe malware, the name of which derives from ‘malicious software’. For the purposes of this paper, the following description will be adopted:
Malware is a piece of software with unwanted functionality.
The variety of known and unknown malware is part of the reason why detecting it is a difficult task. Categorizing malicious code has increasingly become more complex as newer versions appear to be combinations of those that belong to existing malware families [10].
A technique very commonly used in malware is binary obfuscation. Obfuscation is a technique that makes binary and textual data unreadable. Its implementation can be as simple as a few bit manipulations, and as advanced as cryptographic standards [11].
Absolute protection against malware can only be obtained by absolute isolationism [12]. However, this is an unacceptable solution nowadays, when everything is connected.
Software tools used to protect against malware infections currently include intrusion detection systems (IDSs) and anti-virus software (AV). IDSs are used to detect intrusions of all kinds, not just malware. They often compare the pattern of a program flow against a database of patterns of known attacks. This method is called signature-based detection.
Signature-based AV is a very important piece of modern AV multi-layer protection strategy. In the context of anti-virus, ‘signature-based’ means that files are marked or identified as either benign or malicious by comparing them against a database of binary patterns of known malware. The greatest problem with this method is that new malware needs to be discovered and analysed prior the effective detection.
Another method is anomaly-based detection, where intrusions are detected by identifying deviations from the expected behaviour of the program at runtime.
Naturally, it is desirable that all computer systems have the ability to make decisions about which programs are allowed to execute certain functions or call certain system information based on the actions each program will take. Unfortunately, any policy based on such requirements is almost untenable because trying to determine whether a program will perform malicious actions is a generally undecidable problem, also known as the ‘halting problem’, which will be described in the following section.
Rice’s theorem postulates that, whatever property of programs we’re interested in, one cannot write a program that determines for each program whether it satisfies that property. We can reduce Rice’s theorem to the halting problem.
The halting problem postulates that we cannot know if the computation of a program on some input will ever terminate. The importance of the undecidability of the halting problem lies in its generality.
First of all, a device that is capable of computing the solution to any problem that can be computed, provided that the device is given enough storage and time for the computation to finish, is defined as a universal computing machine – also known as a Turing machine.
This device is called a Turing machine because Alan Turing, English logician, was the first to come up with the idea of such a device in 1936. Turing also conjectured that his definition of computable was identical to the ‘natural’ definition. In other words, a problem that cannot be solved by a Turing machine cannot be solved in any systematic manner.
The simplest class of problems to consider are binary problems, i.e. given an input, the output can be ‘yes’ or ‘no’. These problems are known as decision problems and they are formally defined as:
Given an input alphabet Σ and a subset A of Σ*, where Σ* is a set of finite strings formed by concatenating elements of Σ along with the start string ' ', determine whether x ∈ Σ* is in A.
The set L(M) = {x ∈ Σ* : accepts x} is called the language of the Turing machine M that will accept x, whether x ∈ A. The language A is recognizable if there is a Turing machine M with L(M) = A. A is co-recognizable if Σ* - A is recognizable. And if a language is recognizable and corecognizable, then it is decidable.
To determine that a given program Φ is malware, it needs to be shown that at least one undesirable function exists in the code. That can be described as a binary problem, as the answer would be ‘yes, the program is malicious’ or ‘no, the program is clean’.
The question here is whether the machine that computes the answer will ever find an answer or will keep computing forever.
Since we are interested in finding out-of-bounds system calls, Rice’s theorem says that there is no program that will give a correct answer all the time. The program will sometimes fail or never stop computing.
Today, the analysis of a program’s behaviour is often a tedious manual process: when a new piece of potentially malicious code is found, the analyst runs the program in a virtual machine and observes it. If nothing happens in the first moment, one could assume that a trigger condition exists and may not have been met. If suspicions remain, disassembly of the program will be performed and a mental model of the program’s execution can be built. Furthermore, the analyst will try to guess what kind of input or system setup could trigger the malicious code. The process will be repeated until the analyst runs out of patience, time, or is lucky enough to uncover the trigger-based behaviour. In this paper, system calls are defined as iterations between a new piece of software and the base system.
In behaviour-based malware detection the most important input is the knowledge of a malicious behaviour. In anomaly-based detection, the inverse of this knowledge is used in a learning phase. This enables the detector to identify anomalous behaviour by its deviation from normal behaviour. Once the detector has obtained the knowledge, one can employ its detection technique.
The standard program behaviour is given by sequences of system calls. The execution traces of these system calls are collected and the program interactions can be monitored.
The problem with dynamic analysis tools is that only a single path is observed. However, it is possible to trigger certain malicious calls under specific circumstances, e.g. if the program is running in a sandbox, the clock tick is not the same as it would be in a fully operational system and the malicious code won’t be triggered after a clock check. Another example of limitation from the standard program behaviour analysis would be a connection check:
Example of sending a ping:
There is more than one way to send a ping using system calls. To solve this limitation, an abstraction of it is needed. The detection system should allow the exploration of multiple execution paths and the identification of malicious calls under special triggers.
Most of the existing systems for automated malware analysis only allow the tracking of the system calls that are invoked from a single path, like ‘sandboxes’. Unfortunately, this is just a small part of the complete program behaviour. To obtain different executions paths for the same program, some branching points are chosen on the basis of system calls made previously. This will provide a better overview of the code’s actions and a set of trigger conditions.
Before starting to design a solution, it is important to notice how triggers are implemented in high level languages. They are often implemented as conditional jumps depending on inputs from trigger types such as time, return values of network requests, keyboard layouts, and so on.
Malicious threats are triggered if the conditional jump evaluates to the designated direction, e.g. April Fool’s Day Malware that is only launched on 1 April.
The trigger condition is the set of conditions which the trigger input needs to satisfy in order for the code execution to go down the path to the malicious code. The values of the trigger input set satisfying the trigger condition are called trigger values.
The system calls symbolic execution can be used to automatically explore the trigger-based behaviour in the program based on the given trigger types.
Static analysis is a commonly used tool in malware detection. For most object-oriented codes, static analysis works directly on the binary code and performs various analyses, such as reconstruction of the class hierarchy and method calls, and (most importantly for dynamic detection) extracts the control flow and data flow information.
The control flow and the semantics of the program need to be developed in order subsequently to choose the parts of the binary that should be used in the detection. For that, the binary needs to be parsed to a control flow graph. After that, the branching points of the control flow graph are chosen based on the return value of the former requested system calls.
These branching points in the program execution are chosen in such a way that all the alternatives are interesting for being dependent on the system call returning value.
The symbolic execution of the program generates a structural coverage of its control flow based on constraint analysis of the multiple paths. This means that it is possible to determine at time t a set of conditions necessary to take the branch b or not. Every variable on our graph is represented as a symbolic value and each branch is now represented as a constraint solution set. This way, the symbolic execution with the aid of constraint solvers allows the program to go from an entry point EP to a end point END.
In particular, the system calls found in code – the trigger inputs – are represented symbolically and the instructions that depend on these system calls return values which also operate on symbolic values and therefore are executed symbolically.
The key idea behind a classical symbolic execution is to use symbolic values as input values instead of actual data, representing the values of program variables as symbolic expressions, so that the outputs computed are expressed as functions of the symbolic inputs.
During the symbolic execution, a symbolic state is maintained, mapping the program variables to symbolic expressions. Furthermore, a constraint symbolic path SP is now dislocked as a first order free formula over symbolic expressions. The SP aggregates constraints on the inputs that trigger the execution to follow the associated path. At every conditional statement, i.e. if (condition) branch1 else branch2, SP is updated with conditions on the inputs to choose between alternative paths on these branches. With the assistance of a constraint solver, a new path condition SP* is created and initialized to SP ∧ ¬φ(condition) and SP is updated to SP∧φ(condition), where φ(condition) denotes the symbolic predicate obtained by evaluating condition in symbolic state φ. If SP* becomes unsatisfiable, symbolic execution terminates along the corresponding path.
Whenever symbolic execution along a path terminates – with or without error – the current SP is solved and the solution forms the acceptable input set. This shows that, if the program is executed on these concrete inputs, it will take the same path as the symbolic execution did and terminate.
For code containing loops or recursion that may result in an infinite number of paths, generalized symbolic execution is used. Generalized symbolic execution will extend the classical symbolic execution with the ability of handling multithreading and program fragments. The input of multithreading fragments of a program are then recursive data structures.
In the generalized symbolic execution the input is handled in recursive data structures by using lazy initialization, starting the execution of the method on inputs with uninitialized fields and non-deterministically initialized fields when they are first accessed during the function’s symbolic execution.
In many cases, the satisfiability solver may not be able to return an answer to the constraint problem within a reasonable time. Because of this, it is important in the implementation to set a timeout for the analysis of single paths. It is also important to explore as many different branches and paths as possible.
An additional technical limitation for automatically analysing a piece of malware is that the code is often packed or obfuscated. Code packing is a technique where binary code is statically compressed, combined with decompression code into a single executable, and only decompressed at runtime. This way the malicious code is readable just after unpacking. Often, the decompressed code is available in the memory only during runtime. Sometimes, however, the code can be self-modifying and the decompressed information may be written directly into the program file.
In this case, the unpacking algorithm overwrites the program code itself, dynamically generating the malicious code in a different address where no data was stored before.
As briefly mentioned before, code obfuscation is a technique used to make static analysis difficult, where so-called ‘garbage code’ is added to pollute the overview of the control flow graph. It is one of most widely used techniques for hiding malicious code inside clean programs.
In cases where code packing or code obfuscation are applied, it is difficult, if not impossible, to disassemble the binary code and it is necessary to pre-process the sample.
By disassembling the binary code, the instructions of the program can be parsed into a control flow graph. In order to generate this graph it is necessary to use static analysis techniques. Static analysis can be divided in two parts: intra-procedural and inter-procedural.
Intra-procedural analysis is the analysis performed on a single function, independent from other methods in the program. The function is represented by instructions grouped into static basic blocks.
A static basic block is a sequence of instructions that has exactly one entry point and one exit point. These basic blocks are the representation of the most simple unit of the code and they describe a linear flow of instructions. A non-linear control flow appears only at the end of a basic block. Each instruction that is a target of a branch instruction defines a new basic block. In general, every program can be uniquely partitioned into a set of non-overlapping static basic blocks. Figure 1 shows an example of three basic blocks showing a conditional jump.
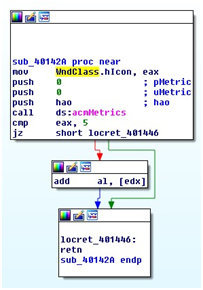Figure 1: Example of three basic blocks (IDA Pro Screenshot) showing a conditional jump.
Whenever it is possible to remove an instruction inside a basic block, it is possible to remove the complete block [13].
The execution path between two basic blocks is parsed in the control flow graph, modelling the relationship and dependence between these two basic blocks. Using the control flow graph and the data-flow analysis, one can determine how values are passed from one block to the next as well as the conditional branch statements, where the execution flow may diverge depending on the value of a variable.
As a certain execution path is desired (the goal is to reach the malicious code) the values for these variables must be constrained. These constraints can then be extracted from the branch instructions.
Inter-procedural analysis is the analysis performed on the entire application as a whole, considering the dependencies and data-flow relationships between different functions. The result of this kind of analysis is a graph, where the values and functions that are used to invoke the next function are modelled.
As the functions are inside basic blocks, one can use these blocks to derive a graph with a possible control flow representation of the processor, where each node is a basic block and the edges represent the control flow among these blocks. Each control flow edge models a dependency between two basic blocks. This graph is called an application’s call graph.
The precision of the graph and the performance of the analysis depend on the options used to generate the control flow edges. The context sensitivity of the graph is an important parameter to consider for the matter of malware detection. The configuration of the precision parameters determines the representation of system calls on the graph. High context sensitivity enables cross references when system calls are invoked in multiple locations. The nodes can then be differentiated by the invoking function, the parameters used for the invocation, or the receiving function [14].
s t a r t ( ) { foo (1 ,10); foo (3 ,20); }
bar (){ foo (1 ,10); }
foo (x , y){ . . some code . .
}
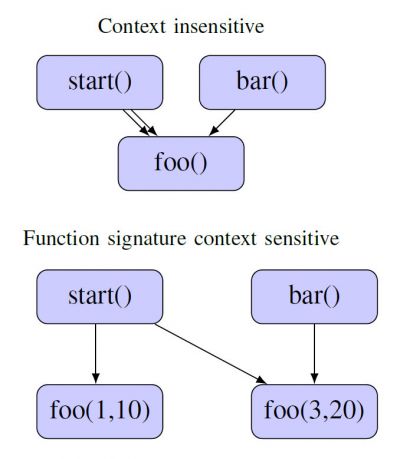Figure 2: Example of context sensitivity for a simple program.
Context sensitivity may also depend on the functions or calls themselves. This means that increasing context sensitivity results in a greater number of system call clones among the graph nodes. Accordingly, it also directly increases the precision of analysis. However, the graph construction may become exponentially resource-intensive for the processor.
In most cases, static analysis is a balance between desired or needed precision and availability of resources.
The analysis of binary code is a non-trivial task. Disassembling and interpreting binary files is complicated for a lot of reasons. One of the most recurrent problems is the ‘Code Discovery Problem’ [15]. In many Instruction Set Architectures (ISAs), binary data and executable instructions are saved in the same way. If the analyst is not able to distinguish between instructions and data, the whole process might be invalidated as some functions may not be discovered or data may be misinterpreted.
Another complication with control flow detection arises if indirect control flow instructions are used inside the binary code. Commonly, control flows are determined by the jump tables that that are generated by the compiler. Typically, the targets of these jumps are easy to compute. Using expression substitution, it is possible to compute the jumps with high precision, allowing the expression to be checked against branch normal forms. Figure 3 shows an example of an application’s control flow graph with high context sensitivity; Figure 4 shows an example of a control flow graph with multiple executable paths for a simple program.
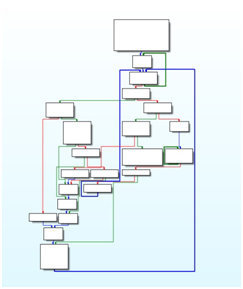Figure 3: Example of an application's control flow graph (IDA Pro Screenshot) with high context sensitivity. The different colours implicate different necessary inputs to trigger the branch.
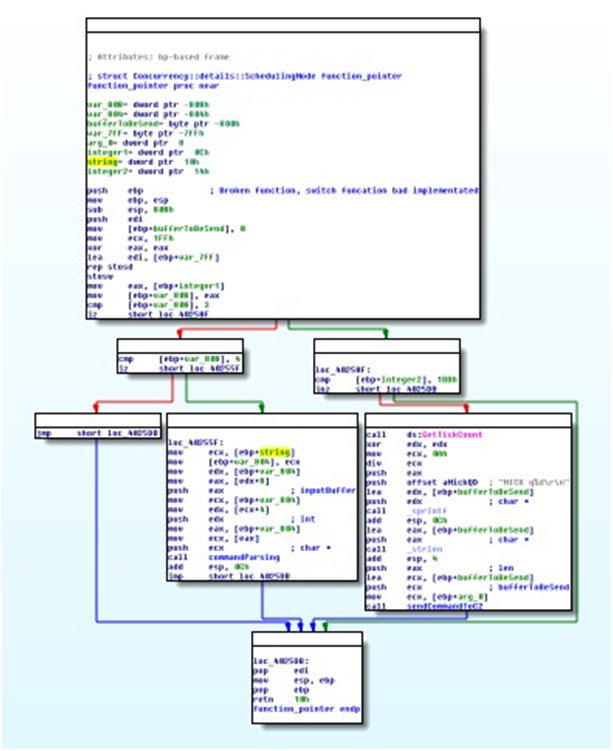Figure 4: Example of a control flow graph (IDA Pro Screenshot) with multiple executable paths for a simple program.
Other sources of indirect control flow are method pointers which are available in most high-level languages, e.g. to implement inheritance or to allow dynamic program behaviour. The targets of this kind of indirect control flow are very hard to compute and until now, no approach could be found which can guarantee the precise detection of all targets.
The instructions in a basic block do not depend on trigger input to operate on concrete values and can be evaluated exactly inside the constraint domain. Thus, symbolic execution builds up symbolic formulas over all symbolic inputs based on the system calls. The mix of concrete and symbolic execution is important for the efficiency of the algorithm, by reducing the formula size this way.
For each path, a mix of concrete and symbolic execution automatically generates constraint formulas. Each of these formulas represents conditions that the trigger input needs to satisfy in order to take the malicious code execution path. With the aid of a SAT/SMT solver (e.g. Z3) it is possible to decide if the constraint formula can be true. If the formula is true then there is at least one set of input values which satisfies the constraint formula. If the solver returns false, it is an indicator that the chosen analysed path is not feasible.
This process is repeated for all paths acquired. Afterwards, a set of satisfiable formulas is generated. Each of the satisfiable formulas in this set represents a trigger condition of a newly discovered path. Each of these paths depends on the system calls. Hence, the solver is able to build the trigger values (i.e. the used system calls) and the values for the trigger inputs, which are necessary to observe the malicious code.
By iterating the process described above, it is possible to automatically explore multiple code paths to discover the system calls of trigger-based behaviours in the program [16].
Greater precision can be achieved afterwards with dynamic analysis. Here, the program is at first symbolically executed. As data is propagated between variables, an expression is created that can reconstruct the variable value from input parameters. When a conditional branch statement is encountered, the symbolic expression of the predicate variables and the conditional expressions extracted from the branch instruction can be transformed into a constraint. This constraint sets the domain for outputs of the branch. For every branch to be fully explored, the input is manipulated in such a way that all constraints are satisfied.
Figure 5: Example of symbolic execution for simple program.
Storage of symbolic information that is gained dynamically is also resource intensive. Gathering the symbolic information is time consuming and recording this information requires plenty of memory. Therefore, to solve every constraint and explore all branches in a program can be an impossible task.
As mentioned before, solving all constraints is a resource-intensive process. Because of this, static analysis is performed: first, to identify the locations in code where suspicious behaviours are possible, and second, to identify the paths that lead to these behaviours.
The control flow graph is generated using the system calls as starting points for the code transversal [17]. This transversal is done for every system call found in the code. With the aid of this transversal, it is possible to identify system calls that cannot lead to suspicious API invocations. Suspicious invocations are defined as all API invocations that are not in the standard behaviour set.
For every suspicious behaviour found, a suspicious path is extracted, containing the sequence of method invocations from system call entry point to the invocation of the suspicious API.
The presence of a suspicious system call and the existence of a path to the malicious behaviour do not imply that the malicious path can be executed at runtime. To determine if the path is feasible, all constraints of the path need to be verified. All constraints must be satisfied. Because of the additivity, the order of the constraints is not relevant. If, and only if, all constraints are satisfied, the malicious code can be started.
For each function along the suspicious path a check of the child function is executed. The invocation of the next function in the path is checked against the conditional return values right before the branching occurs. To also extract these dependencies, a control and data flow analysis is performed on the control flow graph of every single function.
This control flow analysis will resolve whether the conditional branch affects the execution of the next function, and if so, it will extract the constraints based on the variables used in the predicate of the branch statement. The analysis is performed until the constraint and data flow converge, also supporting loops and recursive functions.
If multiple control flow graph paths are found that lead to the next function invocations, the analysis should combine the extract constraints of each path with a logical OR (∨), indicating that as long as one path is satisfied, the suspicious behaviour will be executed.
After all functions have been analysed, the constraints for every function are combined using the full context sensitivity.
Sometimes, it can happen that variables extracted for the constraints do not belong to functions that are part of the path. These constraints must still be extracted, as their return values affect the execution of the path.
SMT solvers are becoming an integral part of a security engineer’s tool kit. The presented work shows why solvers do a remarkable job in assisting malware analysts. The support in deciding whether suggested solutions are valid in their respective problem space saves both economic resources and the time of experts. Solvers support analysts looking for code vulnerabilities and analysing malicious code, detecting vulnerabilities in web applications and breaking encryptions.
Yet, solvers are not suited for generating domain-specific problem descriptions. The preliminary constraint generation step still has to be performed outside the solver.
Important work that should be focused on in the future are:
SMT-based implementations on which I have worked before are:
SMT-based implementations on which I am currently working are:
Lots of research has been done on binary analysis as well as on symbolic execution engines. Many tools have been built on top of KLEE [18] for code verification and tainted analysis. Also other symbolic execution frameworks have been built on top of Z3 [19], like angr [20] and manticore [21]. This work uses the same concepts but focuses on malware analysis.
[1] Freuder, E. C. In pursuit of the holy grail. Constraints, vol. 2, no. 1, pp. 57–61, Apr 1997. https://doi.org/10.1023/A:1009749006768.
[2] Rossi, F.; Beek, P. V.; Walsh, T. Handbook of constraint programming. Elsevier Science, 2006.
[3] Hentenryck, P. V. Constraint Satisfaction in Logic Programming. MIT Press, 1989.
[4] Dechter, R. On the expressiveness of networks with hidden variables. pp.1:556–562, 1990.
[5] Kumar, V. Algorithms for constraint satisfaction problems: A survey. p.1:3244, 1992.
[6] Sebastiani, R. Lazy satisability modulo theories. pp.3–4:141–244, 2007.
[7] Maryellen, M. S. S.; MacDonald, C. Handbook of Psycholinguistics, 2nd ed. Elsevier Ltd, 2006.
[8] Siddharth Agarwal, A. K. Functional smt solving with z3 and racket. FormaliSE, 2013. https://www.cse.iitk.ac.in/users/karkare/pubs/icsews13formaliseid1-p-16138-preprint.pdf.
[9] Garey, M. R.; Johnson, D. S. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York, NY, USA: W. H. Freeman & Co., 1979.
[10] McGraw, G.; Morrisett, G. Attacking malicious code: A report to the infosec research council. IEEE Software, 2000.
[11] Collberg, C.; Thomborson, C.; Low, D. Manufacturing cheap, resilient, and stealthy opaque constructs. In Proceedings of the 25th ACM SIGPLAN-SIGACT symposium on Principles of programming languages. ACM, 1998, pp.184–196.
[12] Cohen, F. Computer viruses – theory and experiments. pp.22–35, 1987.
[13] Hex-RaysSA. The Interactive Disassembler Help Index. 2015. https://www.hexrays.com/products/ida/support/idadoc/.
[14] Reps, T.; Horwitz, S.; Sagiv, M. Precise interprocedural dataflow analysis via graph reachability. In Proceedings of the 22Nd ACM SIGPLANSIGACT Symposium on Principles of Programming Languages, ser. POPL ’95. New York, NY, USA: ACM, 1995, pp.49–61. http://doi.acm.org/10.1145/199448.199462.
[15] Wartell, R.; Zhou, Y.; Hamlen, K. W.; Kantarcioglu, M.; Thuraisingham, B. Differentiating code from data in x86 binaries. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 2011, pp.522–536.
[16] Bardin, S.; Kosmatov, N.; Cheynier, F. Efficient leveraging of symbolic execution to advanced coverage criteria. In Software Testing, Verification and Validation (ICST), 2014 IEEE Seventh International Conference on. IEEE, 2014, pp.173–182.
[17] Thierry, A. Desassemblage et dtection de logiciels malveillants auto-modifiants. Ph.D. dissertation, Universit de Lorraine 2015, 2015, thse de doctorat dirige par Marion, Jean-Yves Informatique Universit de Lorraine 2015. http://www.theses.fr/2015LORR0011.
[18] Cristian Cadar, D. E.; Dunbar, D. Klee: Unassisted and automatic generation of high-coverage tests for complex systems programs, 2008.
[19] Moura L. D.; Bjørner, N. Z3: An efficient smt solver. In Proceedings of the Theory and Practice of Software, 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, ser. TACAS’08/ETAPS’08. Berlin, Heidelberg: Springer-Verlag, 2008, pp.337–340. http://dl.acm.org/citation.cfm?id=1792734.1792766.
[20] Shoshitaishvili, Y.; Wang, R.; Salls, C.; Stephens, N.; Polino, M.; Dutcher, A.; Grosen, J.; Feng, S.; Hauser, C.; Kruegel, C.; Vigna, G. Sok: (state of) the art of war: Offensive techniques in binary analysis. 2016.
[21] Mossberg, M. Manticore: Symbolic execution for humans. 2017. https://blog.trailofbits.com/2017/04/27/manticoresymbolic-execution-for-humans.
[22] Ligh, M. H.; Case, A.; Levy, J.; Walters, A. The Art of Memory Forensics: Detecting Malware and Threats in Windows, Linux, and Mac Memory, 1st ed. Wiley Publishing, 2014.
[23] Hentenryck, P. V.; Michel, L. Constraint-based local search. MIT Press, 2005.
[24] Codognet, P.; Diaz, D. Yet another local search method for constraint solving. Lecture Notes in Computer Science, 2001.
[25] Russinovich, M. E.; Solomon, D. A. Microsoft Windows Internals, Fourth Edition: Microsoft Windows Server(TM) 2003, Windows XP, and Windows 2000 (Pro-Developer). Redmond, WA, USA: Microsoft Press, 2004.
[26] Eilam, E.; Chikofsky, E. J. Reversing: secrets of reverse engineering. Indianapolis (Ind.): Wiley, 2005. http://opac.inria.fr/record=b1133490.
[27] Howe, J. M.; King, A. A pearl on sat solving in prolog. FLOPS 2010, vol. 6009, no. 1, pp.165–174, 2010.
[28] Stephens, N.; Grosen, J.; Salls, C.; Dutcher, A.; Wang, R.; Corbetta, J.; Shoshitaishvili, Y.; Kruegel, C.; Vigna, G. Driller: Augmenting fuzzing through selective symbolic execution. 2016.
[29] Shoshitaishvili, Y.; Wang, R.; Hauser, C.; Kruegel, C.; Vigna, G. Firmalice – automatic detection of authentication bypass vulnerabilities in binary firmware. 2015.
[30] Cifuentes, C.; Sendall, S. Specifying the semantics of machine instructions. p.126. 1998. http://dl.acm.org/citation.cfm?id=580914.858217.
[31] Khattak, S.; Ramay, N.; Khan, K.; Syed, A.; Khayam, S. A taxonomy of botnet behavior, detection, and defense. p.16:898924, 2014.
[32] Szor, P. The Art of Computer Virus Research and Defense. Addison-Wesley Professional, 2005.
[33] Cadar, C.; Sen, K. Symbolic execution for software testing: Three decades later. Commun. ACM, vol. 56, no. 2, pp.82–90, Feb. 2013. http://doi.acm.org/10.1145/2408776.2408795.
[34] Djoudi, A.; Bardin, S. Binsec: Binary code analysis with low-level regions. In Proceedings of the 21st International Conference on Tools and Algorithms for the Construction and Analysis of Systems – Volume 9035. New York, NY, USA: Springer-Verlag New York, Inc., 2015, pp.212–217.
[35] Hai, N. M.; Ogawa, M.; Tho, Q. T. Obfuscation Code Localization Based on CFG Generation of Malware. Cham: Springer International Publishing, 2016, pp.229–247.
[36] Vanegue, J.; Heelan, S.; Rolles, R. Smt solvers in software security.” in WOOT, 2012, pp.85–96.
[37] Filiol, E. Malware pattern scanning schemes secure against black-box analysis. Journal in Computer Virology, vol. 2, no. 1, pp.35–50, 2006. http://dx.doi.org/10.1007/s11416-006-0009-x.
[38] Menezes, A. J.; Vanstone, S. A.; Oorschot, P. C. V. Handbook of Applied Cryptography, 1st ed. Boca Raton, FL, USA: CRC Press, Inc., 1996.
[39] Skowyra, R.; Casteel, K.; Okhravi, H.; Zeldovich, N.; Streilein, W. Systematic analysis of defenses against return-oriented programming. In International Workshop on Recent Advances in Intrusion Detection. Springer, 2013, pp.82–102.
[40] Bennett, J. T. The number of the beast. 2013. https://www.fireeye.com/blog/threatresearch/2013/02/the-number-of-the-beast.html.
[41] Constantin, L. Adobe confirms zeroday exploit bypasses adobe reader sandbox. 2013. http://www.pcworld.com/article/2028163/adobeconfirms-zeroday-exploit-bypasses-adobe-readersandbox.html.
[42] McKinney, W. Python for data analysis. Beijing, Cambridge, Farnham: O’Reilly, 2012, 2013. http://opac.inria.fr/record=b1133860.
[43] Stallings, W. Operating Systems: Internals and Design Principles, 6th ed. Upper Saddle River, NJ, USA: Prentice Hall Press, 2008.
1 A decision problem is NP-complete when it is in both NP and NP-hard. The set of NP-complete problems is often denoted by NP-C or NPC. The abbreviation NP refers to ‘non-deterministic polynomial time’.
2 For more examples, see https://yurichev.com/writings/SAT_SMT_by_example.pdf.
